Komplexe Planungsprobleme – Effektiver Einsatz von OptaPlanner

Das Lösen von Planungsproblemen ist eine Herausforderung, der sich viele Unternehmen, z. B. entlang einer Supply Chain, regelmäßig stellen müssen. Welche Puffer sollten eingehalten werden, um mit Maschinenausfällen umgehen zu können? Wie sollen die Touren einer Fahrzeugflotte gestaltet werden, damit die Auslieferung von bestellten Gütern möglichst kostengünstig ist? Wie sieht eine geeignete Schichtenplanung unter Einhaltung gesetzlicher Regelungen aus?

Schnell werden die Fragestellungen so komplex, dass eine technische Unterstützung durch geeignete Software notwendig wird.

Open-Source-Solver wie OptaPlanner ermöglichen Entwickler:innen eine geeignete Softwarelösung für Planungsprobleme umzusetzen. Dabei müssen sie keine Spezialist:innen für mathematische Problemmodellierung oder entsprechende Optimierungsalgorithmen sein. Damit ein solches Framework zum gewünschten Ergebnis führt, muss es effektiv und im Bewusstsein möglicher Einschränkungen und Herausforderungen eingesetzt werden.

Mit diesem Artikel möchten wir Ihnen helfen, typische Missverständnisse und Stolperfallen beim Einsatz von Planungssoftware wie OptaPlanner zu vermeiden.

Insbesondere legen wir Ihnen die folgenden beiden Strategien ans Herz:

• Binden Sie Entscheider in den Umsetzungsprozess mit ein, damit das fachliche Problem auch richtig abgebildet wird! Kommunikation und iteratives Vorgehen sind maßgeblich für den Erfolg.
• Tendenz: Je länger das Optimierungsverfahren läuft und je mehr verschiedene Verfahren Sie ausprobieren, desto besser ist das Endergebnis. Nutzen Sie Konfigurationsbeispiele und ausgiebige Experimente, um das beste Maß an Aufwand und Output für Ihre Problemstellung zu finden.

Optaplanner – etabliert und effektiv

OptaPlanner ist ein Open-Source Java Framework und arbeitet mit Heuristiken und Metaheuristiken, um die definierten Planungsprobleme zu lösen.

Heuristische Verfahren können die beste Lösung als Ergebnis nicht garantieren, dafür stellen sie keinerlei mathematischen Anforderungen an das zu lösende Problem und lassen sich auch auf komplexe Probleme anwenden. Unter gegebenen – meist zeitlichen – Einschränkungen und durch wiederholtes Anwenden bestimmter Regeln versucht ein heuristisches Verfahren eine möglichst gute Lösung zu finden. In jedem Schritt bewertet OptaPlanner mit Hilfe einer Bewertungsfunktion eine mögliche Lösung des Planungsproblems und versucht diese Lösung Schritt-für-Schritt, d. h. iterativ, zu verbessern. Beim Anwenden der Regeln zur Anpassung einer Lösung spielt nicht zuletzt auch der Zufall eine Rolle.

Metaheuristiken bilden ein übergeordnetes, problem-unabhängiges Framework zum Lösen von Planungsproblemen. Verschiedene Metaheuristiken bieten dabei unterschiedliche Strategien, um den Lösungsraum zu durchsuchen und das Ergebnis zu verbessern.

Die Anwender:innen von OptaPlanner sind dafür zuständig, das Planungsproblem als sogenanntes “Domain Model” zu implementieren, die Bewertungsfunktion (“Scoring Function”) zu definieren und die angewandten Verfahren auszuwählen (“Solver Configuration”).

Ein Beispiel – Das Tourenplanungsproblem

Es gibt verschiedene Varianten des Tourenplanungsproblems. Im Kern geht es immer darum, die Routen von Fahrzeugen zwischen verschiedenen Standorten festzulegen. Dabei starten die Fahrzeuge an einem bestimmten Standort, zum Beispiel einem Depot. Die Zwischenziele einer Route könnten Kund:innen sein, denen eine Warenbestellung geliefert wird. Planungsprobleme unterscheiden sich in Rahmenbedingungen wie der Anzahl der Bestellungen, der Anzahl und Kapazität der Fahrzeuge oder auch im Vorhandensein von Lieferzeitfenstern.

Bei der Lösung des Planungsproblems sind verschiedene Ziele möglich. Sollen die variablen Lieferkosten oder die Anzahl an Fahrzeugen minimiert werden? Müssen dabei alle Bestellungen ausgeliefert werden oder können wir im Sinne der Profitmaximierung vielleicht sogar Bestellungen auswählen?

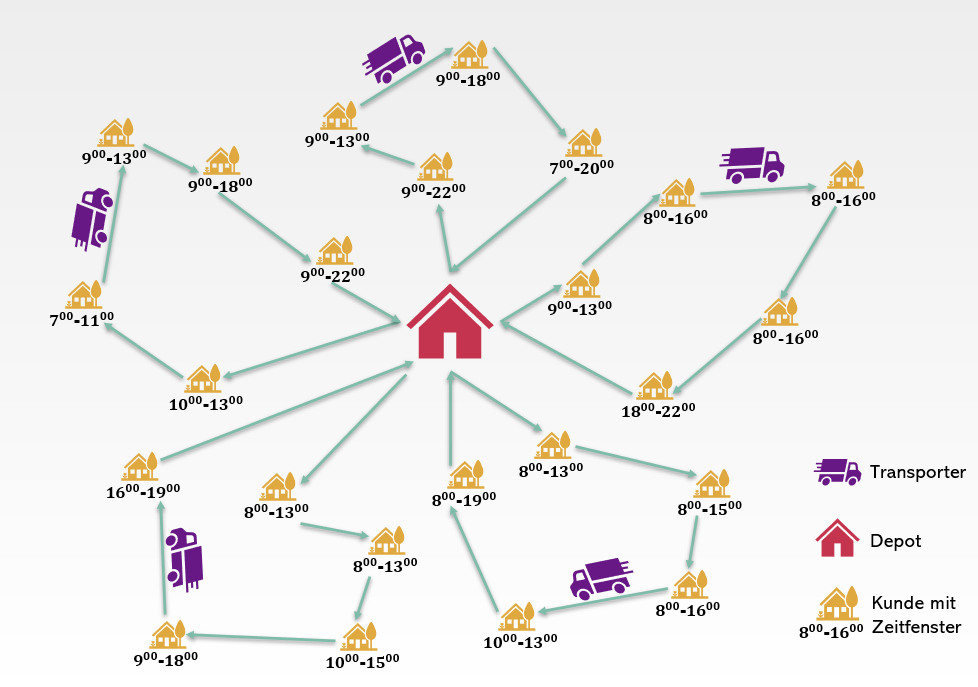
Bei OptaPlanner dient die sogenannte Bewertungsfunktion (“Scoring Function”) dazu, einer möglichen Lösung, d. h. einem möglichen Tourenplan, einen Wert zuzuordnen. Sie soll sicherstellen, dass eine Lösung den Vorstellungen der Entscheider:innen entspricht. So sind Ziele wie die Minimierung der Lieferkosten als sogenannte “Soft Constraints” zu hinterlegen: Jede Auslieferung ist mit zusätzlichen Kosten verbunden. Diese Kosten sollen aber möglichst gering bleiben. Im Gegensatz dazu gibt es auch sogenannte “Hard Constraints”. Diese müssen erfüllt werden, damit eine Lösung überhaupt gültig ist. Zum Beispiel kann die Kapazität von Fahrzeugen nicht überschritten werden.

Die Scoring Function – Essentiell und kritisch

Die Bewertungsfunktion spielt eine bzw. DIE wesentliche Rolle bei der Umsetzung des Planungsproblems. Einerseits muss sie das fachliche Problem geeignet abbilden, damit das Lösungsverfahren - die Metaheuristik - in die richtige Richtung läuft. Andererseits ist die Auswertung der Funktion der hauptsächliche "Kostentreiber", d. h. sie bestimmt den zeitlichen Aufwand bzw. die mögliche Anzahl an Iterationen zur Bildung einer guten Lösung. Während die Verfahren zur Lösung des Problems von OptaPlanner bereitgestellt werden, ist die Aufstellung der Bewertungsfunktion ein wichtiger und gleichzeitig herausfordernder Schritt für die Anwender:innen, da die Bewertung problemspezifisch ist und somit individuell festgelegt werden muss.

Dabei müssen sich Entwickler:innen zwei Herausforderungen stellen. Erstens ist die Möglichkeit des effizienten Auswertens der Bewertungsfunktion maßgeblich für den Erfolg der Optimierung. Wenn die Optimierung zeitlich begrenzt ist, kommt es darauf an, wie viele verschiedene Lösungen pro Zeiteinheit betrachtet und bewertet werden können. (Wir verweisen dafür auf unseren Blogartikel zu ConstraintStreams).
Doch diese eher technische Fragestellung ist nur ein Schritt. Im Folgenden gehen wir auf eine weitere Herausforderung ein: Wie bilde ich das fachliche Problem geeignet ab?

Die Qualität des Ergebnisses steht und fällt mit den Constraints

Betrachten wir zum Beispiel ein Tourenplanungsproblem mit Lieferzeitfenstern. Hierbei könnte es Ziel von Lieferat:innen sein, Bestellungen möglichst kostengünstig auszuliefern. Kosten definieren sich dabei über einen Distanz-abhängigen, variablen Betrag. Das bedeutet, je mehr Strecke ein Lieferfahrzeug zurücklegen muss, desto teurer ist der Einsatz. Diese Kosten sind in der Bewertungsfunktion eines möglichen Lieferplans abzubilden, in OptaPlanner also über die sogenannten Soft Constraints. Die Kosten fallen an und man möchte sie minimieren.

Schauen wir uns nun einmal an, wie das Soft Constraint “Kostenminimierung” mit der Nebenbedingung der Lieferzeitfenster zusammenspielt. Durch unterschiedliche Abbildung der Lieferzeitfenster als Hard- und Soft Constraint können wir das Optimierungsergebnis in verschiedene Richtungen lenken.

Szenario 1: Zeitfenster als Hard Constraint (Fokus auf ein Ziel)

Nun könnte es sein, dass die Lieferzeitfenster streng eingehalten werden müssen und dies somit eine Bedingung für einen akzeptablen Lieferplan ist. In einem solchen Fall wären die Lieferzeitfenster als “Hard Constraints” zu behandeln und das Ziel der Kostenminimierung unter Einhaltung der Lieferzeitfenster zu verfolgen.

rule "AnkunftNachFrist"
    when
        KundeMitZeitfenster(endzeit < ankunftszeit, $endzeit : endzeit, $ankunftszeit : ankunftszeit)
    then
        scoreHolder.addHardConstraintMatch(kontext, $endzeit - $ankunftszeit);
end

Szenario 2: Zeitfenster als Soft Constraint (Gleichzeitige Abwägung mehrerer ziele)

Alternativ könnte die Nicht-Einhaltung von Lieferzeitfenstern auch „nur“ zur schlechteren Bewertung eines Lieferplans führen, ihn aber nicht gleich als Lösung ausschließen. In einem solchen Falle wären die zusätzlichen Lieferkosten aufgrund von Umwegen zur Einhaltung der Zeitfenster einzelner Kund:innen (Soft Constraint: Kostenminimierung) mit den Konsequenzen verspäteter Lieferungen (Soft Constraint: Lieferzeitfenster) abzuwägen.

Aber wie kann eine solche verspätete Lieferung bewertet und mit Lieferkosten ins Verhältnis gesetzt werden? Verspätete Lieferungen können unzufriedene Kunden und damit reduzierten, zukünftigen Umsatz zur Folge haben. Soll das Planungsproblem mit einer Software gelöst werden, muss der Effekt einer solchen Unzufriedenheit quantitativ abgebildet werden – und ins Verhältnis gesetzt werden mit den Kosten der Lieferung. Es werden mehrere Ziele gleichzeitig betrachtet.

Das Beispiel von oben könnte folgendermaßen abgewandelt werden, sodass das Hard Constraint zum Soft Constraint wird:

rule "AnkunftNachFrist"
   when
       KundeMitZeitfenster(endzeit < ankunftszeit, $endzeit : endzeit, $ankunftszeit : ankunftszeit)
   then
       scoreHolder.addSoftConstraintMatch(kontext, $endzeit - $ankunftszeit);
end

In dieser Variante würde nun der Wert eines Fahrplans folgendermaßen bestimmt:

Wert des Fahrplans = gefahrene Distanz der Fahrzeuge + Verspätungszeit (jeweils in Minuten)

Aber ist der Wert einer Minute Verspätung genauso groß wie der Wert einer Minute Fahrzeit? Die Kosten der Lieferung können in Euro pro Kilometer oder Euro pro Minute ausgedrückt werden. Wie viel Euro kostet aber eine Minute Verspätung? Denn: OptaPlanner summiert nur die Werte der Soft-Constraint Treffer, den Effekt der einzelnen Komponenten müssen Anwender:innen geeignet umsetzen.

Szenario 3: Zeitfenster als stark gewichtetes Soft Constraint

Alternativ könnte das Soft Constraint auch folgendermaßen angepasst werden: Durch die Ergänzung eines Faktors, wie hier z. B. der 10, fällt das jeweilige Soft Constraint stärker ins Gewicht.

rule "AnkunftNachFrist"
   when
       KundeMitZeitfenster(endzeit < ankunftszeit, $endzeit : endzeit, $ankunftszeit : ankunftszeit)
   then
       scoreHolder.addSoftConstraintMatch(kontext, 10*($endzeit - $ankunftszeit));
end

Auf diese Weise kann ein Soft Constraint sogar in Richtung des Effekts eines Hard Constraints manipuliert werden. Nun wäre eine Minute Verspätung so „teuer“ wie 10 Minuten Fahrt.

Ist diese Abbildung „richtiger“? Dies kann nicht pauschal beantwortet werden und ist abhängig vom jeweiligen Anwendungsfall. Wichtig ist hier, dass den Anwender:innen die Effekte der Umsetzungsentscheidungen bewusst sind. Diese Frage können Entwickler:innen alleine nicht beantworten und der enge Austausch mit einem fachlichen Entscheider ist notwendig.

Aufbereitung der Ergebnisse als Entscheidungsvorlage

Je nach Umsetzung als Hard oder Soft Constraint ergeben sich unterschiedliche Ergebnisse. Diese sollten nebeneinandergelegt und in einer Entscheidungsvorlage geeignet aufbereitet werden. Auf dieser Grundlage können Entscheider:innen dann eine informierte Auswahl der konkreten Konfiguration tätigen.

In der folgenden Tabelle sind die beispielhaften Ergebnisse einer bestimmten Metaheuristik, der Tabu-Suche für die drei verschiedenen Zeitfenster-Szenarien bei 400 Kunden und 100 Fahrzeugen aufbereitet (OptaPlanner-Beispiel: Homberger_0400_R1_4_1, jeweils 5 Minuten Laufzeit).

Der Score hilft Entscheider:innen nicht dabei, eine Lösung fachlich zu bewerten. Es handelt sich um eine technische Kennzahl, die alleinstehend für Stakeholder keine Aussagekraft hat. Dafür sollten die Ergebnisse der fachlichen Kriterien – also die Höhe der Kosten und der Verspätung – graphisch oder wie hier in einer Tabelle angegeben werden. Bei der Umsetzung der Zeitfenster als Hard Constraint (Szenario 1) gibt es keine Verspätung. Dafür ist die gefahrene Gesamtdistanz am größten, damit die individuellen Lieferzeitfenster eingehalten werden können. Wird die Verspätung wie in Szenario 2 weniger stark gewichtet, ist die Gesamtverspätung verhältnismäßig hoch. Maximal wartet ein Kunde sogar 34 Minuten und es gibt 53 Verspätungen insgesamt. Dafür sind die Lieferkosten hier am geringsten. Bei Szenario 3 geht die Verspätung stärker in die Bewertung einer Lösung ein, sodass die Verspätung insgesamt geringer ist als bei Szenario 2.
Nun muss für den Anwendungsfall entschieden werden, welche Umsetzungsvariante das Problem am besten löst.

Bei all diesen Überlegungen ist ein wichtiger Punkt leicht zu erkennen: Entscheider:innen und Umsetzer:innen sollten bei diesem Schritt eng zusammenarbeiten. Denn bei der Definition der Bewertungsfunktion sind viele verschiedene Varianten möglich und eine zielführende, technische Umsetzung ist nur mit geeigneter fachlicher Einschätzung zu erreichen. Entwickler:innen sollten dabei die Ergebnisse aussagekräftig aufbereiten und einen Dialog starten. Dann sind Aussagen wie "Diese Lösung ist ganz gut, hier müssen die Kosten aber noch geringer werden, ein bisschen höhere Verspätung ist ok" möglich. Entwickler:innen können solche Aussagen verwerten und z. B. die Gewichte der Constraints anpassen.

Und dabei wird auch ein zweiter wesentlicher Aspekt deutlich: Die Umsetzung eines solchen Planungsproblems bedarf einer intensiven, iterativen Konfigurations- und Testphase. Oft findet sich die beste Einstellung erst durch die Betrachtung der Ergebnisse verschiedener Alternativen. Eventuell ergeben sich dabei sogar noch neue Kriterien, welche bisher gar nicht betrachtet wurden. Soll in unserem Tourenplanungsproblem zum Beispiel auch die Anzahl der Verspätungen minimiert werden? Warum wurde der CO2-Ausstoß nicht betrachtet? Der Aufwand lohnt sich: Ein einmal gefundenes Setting kann dann zur Lösung verschiedener, konkreter Probleme genutzt werden – zum Beispiel zur Erstellung von Tourenplänen verschiedener Liefertage.

Herausforderung: Konfiguration der Experimente

Eine weitere Herausforderung liegt in der Konfiguration des OptaPlanner-Lösers. Hierbei muss der Entwickler einige Entscheidungen treffen: Welche Algorithmen verwende ich, wie lange sollen sie laufen, kann ich alle verfügbaren Algorithmen bedenkenlos anwenden? Wenn ich die optimale Lösung nicht garantieren kann, wie erhöhe ich die Wahrscheinlichkeit eine möglichst gute zu finden?

OptaPlanner bietet verschiedene Typen von Lösungsverfahren an: neben den angesprochenen Metaheuristiken auch Exhaustive Search und verschiedene Konstruktionsheuristiken (“Construction Heuristics”). Exhaustive Search testet alle möglichen Lösungen im Lösungsraum und sucht sich die beste heraus. Bei großen Problemen nicht anwendbar, lohnt es sich bei ausreichend kleinen das Lösungsverfahren zu verwenden, da es garantiert die beste Lösung findet. In den meisten Fällen aber führt eine Kombination aus Construction Heuristics und Metaheuristics zum besten Ergebnis. Bestes Ergebnis bedeutet in diesem Kontext: Für große, komplexe Probleme wird unter (meist zeitlichen) Einschränkungen eine gute Lösung gefunden. Construction Heuristics stellen eine initiale Lösung zu Verfügung, Metaheuristiken versuchen diese mit verschiedenen Strategien zu verbessern.

Doch wie geht man bei der Konfiguration der verwendeten Metaheuristiken am besten vor und was muss beachtet werden?

Optimierungsprobleme haben unterschiedliche, mathematische Charakteristiken (Problem Landscape und lokale Minima) und die verschiedenen Metaheuristiken können unterschiedlich gut mit diesen individuellen Gegebenheiten umgehen. Nehmen wir als Beispiel die lokalen Minima. Um lokale Minima zu umgehen, sollte man nicht einfach dem Ergebnis des Hill Climbings vertrauen. Andere Verfahren, wie Tabu Search, Simulated Annealing oder Late Acceptance bieten unterschiedliche Strategien lokalen Minima zu entgehen und somit eine bessere Lösung zu finden.

Die Erfahrung hat gezeigt, dass es fast immer besser, wenn nicht sogar notwendig ist, ein Problem nicht nur einmal zu lösen. Wenden Sie verschiedene Verfahren mit unterschiedlichen Strategien auf das Problem an. Dann kann das beste Ergebnis als endgültige Lösung verwendet werden.

Eine wesentliche Rolle spielt bei der Konfiguration auch das Terminierungskriterium. Dieses entscheidet, wann ein Verfahren stoppt und das beste Ergebnis zurückgibt. Hier kann der Entwickler zum Beispiel eine maximale Laufzeit festlegen und zusätzlich einstellen, dass nach einer gewissen Zeit ohne Verbesserung das Lösungsverfahren automatisch abbricht. Eine Überlegung: Lassen Sie lieber ein Verfahren 10 Minuten laufen oder mehrere Verfahren 5 Minuten? Probieren Sie es aus!

An dieser Stelle verweisen wir auf die Beispiele des Optaplanners (...\optaplanner-distribution-7.44.0.Final\examples\sources\src\main\java\org\optaplanner\examples). Mit 24 verschiedenen Beispielen und zusätzlichen Benchmarking-Möglichkeiten, die direkt ausgeführt und angepasst werden können, finden Sie garantiert eine geeignete Konfiguration für Ihren Löser.

Haben Sie ein Planungsproblem, bei welchem wir Sie unterstützen können oder haben Sie das Gefühl, dass OptaPlanner an seine Grenzen stößt? Haben Sie zum Beispiel einen wertvollen Pool an Daten, bei dem Sie vermuten, dass er dabei helfen könnte, ein Verfahren effizienter und problemspezifisch zu definieren? Eventuell brauchen Sie eine dynamische Problemlösung innerhalb von Millisekunden? Verfahren des Data Mining und Machine Learning können hier ihre Stärken ausspielen. Gerne erarbeiten wir gemeinsam eine individuelle Lösung für Sie.