GPGPU-Programmierung & Astronomie

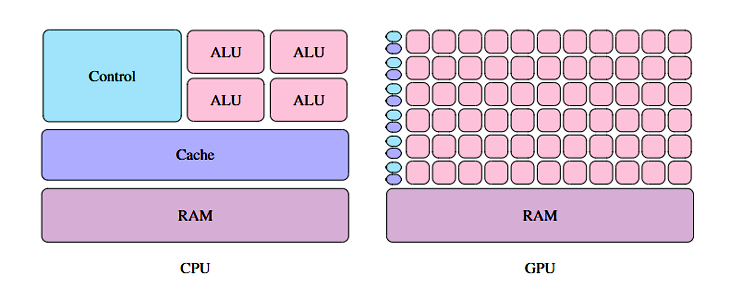
Seit GPUs (Graphics Processing Units) verwendet wurden, um Bitcoin zu farmen, ist allgemein bekannt, dass die ursprünglich für Grafikberechnungen gedachte Hardwarekomponente auch für andere Zwecke eingesetzt werden kann. Im Gegensatz zu CPUs (Central Processing Units) haben GPUs sehr viele kleine ALUs (Arithmetic Logic Units). Um die Architektur von GPUs effizient zu nutzen, müssen alle Recheneinheiten beschäftigt werden. Es ist notwendig, Programme zu schreiben, die Berechnungen parallel ausführen. Deswegen ist der Einsatz von GPUs auch kein Allheilmittel, um schnellere Programme zu schreiben. Algorithmen eignen sich besonders gut dafür, auf GPUs berechnet zu werden, wenn sie aus vielen kleinen unabhängigen Operationen bestehen und die Datenmenge groß ist.

Radioastronomie und Signalverarbeitung

In der Wissenschaft der Radioastronomie werden astronomische Objekte wie Sterne, schwarze Löcher und Galaxien untersucht. Für diesen Zweck werden Radiowellen von Teleskopen empfangen und dokumentiert. Die gesammelten Daten werden verwendet, um die Positionen, Bewegungen und Veränderungen von Himmelsobjekten zu untersuchen. Die Menge an Daten, die dabei produziert wird, ist gigantisch. Das Max Planck Institut für Radioastronomie erwartet, dass die nächste Generation von Teleskopen pro Sekunde fünf Petabits an Daten produziert. Zurzeit produziert das Effelsberg-Teleskop 256 GB/s. Diese Daten sollen möglichst in Echtzeit ausgewertet werden.

Die Auswertung der Daten ist nicht trivial und wird erschwert, wenn die Signale verunreinigt oder undeutlich sind. Ein simples Beispiel für verunreinigte Daten ist die Vermischung von Signalen aus dem All mit elektromagnetischer Strahlung vom 5G Netz; hier müssen unterschiedliche Signalquellen separiert werden.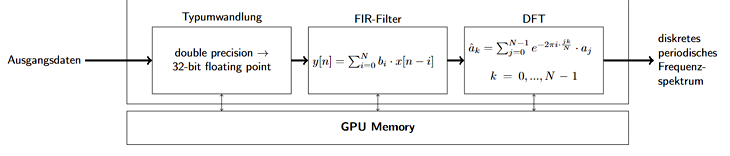

Abbildung1: Exemplarischer PFB-Filter

Dafür werden die Signale mit unterschiedlichen Methoden verarbeitet. Eine Möglichkeit hierfür ist eine Polyphase Filterbank (PFB). In dieser Verarbeitung werden mehrere Schritte kombiniert. Eine abstrakte Realisierung einer PFB ist in Abbildung 1 dargestellt. Dies ist nur ein Beispiel für die Verarbeitung von Teleskopdaten. Hier werden nach einer Typumwandlung ein Filter mit endlicher Impulsantwort (FIR-Filter) und danach die diskrete Fourier-Transformation angewendet, um von den Ausgangsdaten auf leichter zu verarbeitende Daten zu kommen.

FIR-Filter

Die Anwendung eines FIR-Filters erfolgt bei der Signalverarbeitung ähnlich wie bei einem Grafikfilter. Wenn ein Filter auf eine Grafik angewendet wird, wird der Farbwert eines Pixels basierend auf den umliegenden Elementen angepasst. So können Bilder zum Beispiel weichgezeichnet werden wie in Abbildung 2.

Abbildung 2

In der Signalverarbeitung wird eine Zahl, die die Stärke der empfangenen Radiowelle misst, basierend auf anderen Werten geändert. Hierfür werden m nachfolgende Elemente (nicht unbedingt die direkt folgenden) mit verschiedenen Koeffizienten multipliziert und die Summe wird als neues Element geschrieben. Mathematisch lässt sich dies wie folgt ausdrücken:

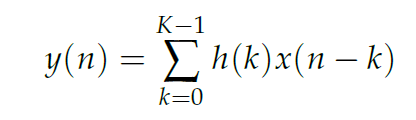FIR-Filter sind besonders gut geeignet, weil sie niemals instabil werden oder zu selbstständigen Schwingungen angeregt werden. Eine beispielhafte Berechnung ist in Abbildung 3 dargestellt. Sowohl die Input-Daten als auch die Koeffizienten sind Gleitkommazahlen. Für die Anwendung des Filters werden zwei Variablen definiert: die Anzahl der Channels und die Anzahl der Taps. Um den neuen Wert von einem Element zu berechnen, werden m folgende Elemente desselben Channels mit den passenden Koeffizienten multipliziert, wobei m die Anzahl der Taps ist. Für einen Input der Größe n werden also m×n Multiplikationen ausgeführt, was dazu führt, dass die Laufzeit Klasse des Filters O(m×n) ist.

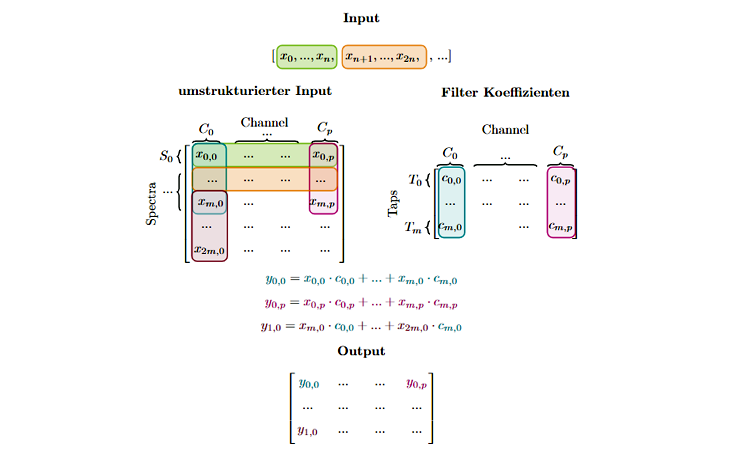
Abbildung 3: FIR-Filter

Diskrete Fourier-Transformation

Die diskrete Fourier-Transformation kann mehrere Zwecke in der Signalverarbeitung haben, z. B. verschiedene Quellen des Signals zu separieren oder einzelne Amplituden der Frequenzen zu bestimmen. Die dargestellte Formel zur Berechnung (2) kann mithilfe der schnellen Fourier-Transformation in der Laufzeit O(n× log 2) berechnet werden. Hier ist n die Anzahl der Elemente.

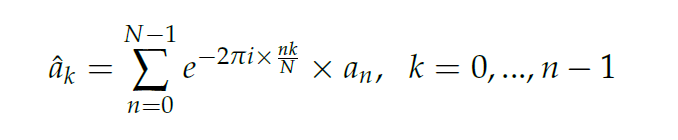
Low- and High-Level-Ansätze

Um Programme für die GPUs zu entwickeln, gibt es verschiedene Ansätze. High-Level-Ansätze abstrahieren von Details wie Speicheroperationen oder der genauen Anzahl von Threads, die gestartet werden. Dadurch lassen sich Programme oft schneller entwickeln als gleichwertige Low-Level-Programme. Zudem sind sie auf unterschiedliche Hardware Architekturen übertragbar und leichter zu warten. Low-Level-Programme sind dafür oft performanter; durch die Details können sie die Hardware maximal ausnutzen. Eine genaue Beschreibung der jeweiligen Implementierungen würde zu viel Platz in Anspruch nehmen. Das High-Level-Programm hat lediglich etwa ein Viertel der Zeilen wie das entsprechende Low-Level-Programm, wobei zusätzlich beachtet werden sollte, dass das High-Level-Programm mehr triviale Operationen wie z. B. Variablenzuweisungen beinhaltet.

Beispielhaft kann das beim Erstellen eines Arrays gezeigt werden: Im Code Beispiel 1 wird ersichtlich, dass für ein Low-Level-Programm sowohl Speicher auf der GPU als auch auf der CPU reserviert werden muss (l. 3,4) und danach die Daten von der CPU auf die GPU kopiert werden. Im entsprechenden High-Level-Programm (Code Beispiel 2) ist die Erstellung desselben Arrays ein Einzeiler; der Speicher wird sowohl auf der GPU als auch auf der CPU reserviert. Der Datentransfer passiert implizit.

1 int size = 42;
2 float* d_input;
3 float* h_input = malloc(size * sizeof(float));
4 cudaMalloc(&d_input, size * sizeof(float));
5 cudaMemcpy(&d_input, h_input * sizeof(float));

Listing 1: Beispielhafte Low-Level Operationen>

1 array<float, 42, dist> input;

Listing 2: Beispielhafte High-Level Operationen

Aus diesem simplen Beispiel können schon Vorteile und Nachteile gezogen werden. Zum einen ist der High-Level-Ansatz weniger flexibel, z. B. kann nicht nur ein Teil des Arrays auf die GPU kopiert oder ein Array nur auf der GPU erstellt werden. Zum anderen braucht der Low-Level-Ansatz mehr Zeit, um geschrieben zu werden.

Ergebnisse

Zunächst ist es wichtig, zu verifizieren, ob ein Programm auf der GPU schneller ist als ein Programm auf der CPU. Als Vergleich wurde eine Referenzimplementierung, die in Python geschrieben wurde, genutzt. Das Low-Level-Programm ist 17-96 Mal so schnell und das High-Level-Programm 5-37 Mal. Damit ist verifiziert, dass sich GPGPU-Programme besser als (single-threaded) CPU-Programme eignen, um das gegebene Problem zu lösen.

Dies ist dargestellt in Abbildung 4. Die x-Achse stellt verschiedene Datengrößen und verschiedene Konfigurationen dar. Hierbei steht die erste Zahl für die Datengröße und die zweite Zahl für das jeweilige Setting an Channels und Taps. 1.x-Settings sind die kleinste Datengröße und 3.x die größte. Hier wird ersichtlich: Je größer die Datenmenge, umso effizienter die GPGPU-Verarbeitung. Außerdem variiert der Unterschied je nach Konfiguration. Die Erklärung dafür ist, dass der FIR-Filter in dem gegebenen CPU-Programm besonders ineffizient ist. x.1-Konfigurationen haben einen rechenintensiven FIR-Filter, x.4-Konfigurationen haben eine rechenintensive Fourier-Transformation.

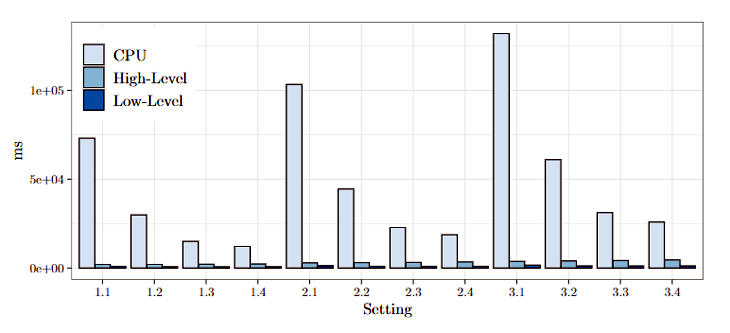
Abbildung 4: Laufzeit CPU and GPU Programme

Um die Daten des Effelsberg-Teleskops zu verarbeiten, eignet sich nur die Low-Level-Implementierung. Hierfür müssen jede Achtelsekunde 1GB an floats verarbeitet werden. Zum Vergleich von Low- und High-Level-Ansätzen lässt sich sagen, dass, wenn die Rechenschritte separat betrachtet werden, in manchen Fällen das Low-Level-Programm besser abschneidet, in anderen Fällen das High-Level-Programm. In der totalen Laufzeit schneidet jedoch immer das Low-Level-Programm schneller ab, da im High-Level-Programm mehr Speicher belegt wird und zusätzliche Datentransfers gemacht werden.

GPGPU-Programmierung ist ein guter Lösungsweg, um Signale in der Radioastronomie zu verarbeiten, da eine große Menge an Daten vorhanden ist und sich die diskutierten Schritte gut parallelisieren lassen. Die Generierung von GPGPU-Code ist performanter als die CPU-Lösung, aber sie ist noch verbesserungsfähig, um näher an die Performance von Low-Level-Programmen heranzukommen.

Alle Programme können in diesem github Repository gefunden werden. 

Hinweis: Dieser Artikel fasst im Wesentlichen Erkenntnisse aus der Abschlussarbeit von Nina Herrmann (WWU Münster, betreut durch Prof. Kuchen, 2019) zusammen.